Бесконечность в бесконечно малом. Искусство самоподобия
2024-01-18 10:24:21, Рубрики:
ФИЛАТЕЛИЯ.РУ
Всем, кто соскучился по красивой математике, Александр Платонов предлагает свою новую статью о том, как можно рисовать картины с помощью формул. Это очень красиво. Особенно в динамике.

* * *
«Под микроскопом он открыл, что на блохе
Живет блоху кусающая блошка;
На блошке той блошинка-крошка,
В блошинку же вонзает зуб сердито
Блошиночка, и так ad infinitum». Джонатан Свифт
Если вы отломите одно из соцветий цветной капусты, то в руках окажется та же капуста, только меньшего размера. Можно продолжать те же действия снова и снова, и каждый раз будут получаться еще более уменьшенные копии той же капусты.

Открывая одну матрешку за другой, мы попадаем в мир простых иерархических самоподобных множеств. Для описания таких систем в математике применяют термин «фрактал». Фракталы – это самоподобные фигуры, которые повторяют свою структуру при увеличении или уменьшении масштаба. Малая часть фрактала выглядит также как и целый фрактал.

Чем так привлекательны изображения? У фракталов дробная размерность! Линия – одномерна, плоскость – двухмерна, объем мы воспринимаем трехмерным. Фракталы принимают, как правило, дробное значение от 1 до 2 или от 2 до 3. Это не линия, не плоскость и не объем, а нечто среднее между ними.

Множество Кантора
Старейшим фракталом считается множество Кантора, одного из основателей теории числового множества. Этот фрактал представляет множество, равное двум копиям самого себя.

Отрезок любой длины делится на три части. Далее вынимается средний участок. На втором шаге подобной процедуры деления на три части с последующим удалением середины подвергаются оба оставшихся отрезка.
Процесс может продолжаться до бесконечности, пока не получится Канторова пыль – множество точек, которые не были удалены.

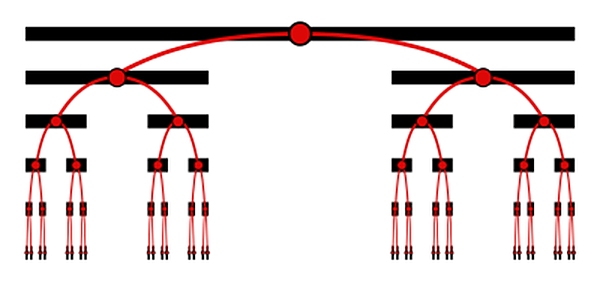
Древовидный фрактал
Строится на линиях путем прибавления на каждом шаге итерации уменьшенной копии предыдущего звена в виде разветвленной ветки. Так растет крона деревьев.

Подобную форму имеет дыхательная, кровеносная и нервная системы.

К природным относятся и фракталы Георга Лихтенберга, немецкого физика, изучавшего природу разрядов молний.

Такие следы оставляют потоки электронов при высоковольтном разряде.

Древовидный фрактал можно построить и на простых геометрических фигурах, например, на единичном квадрате в виде дерева Пифагора. Уменьшение длины стороны квадрата происходит с коэффициентом 0,707.
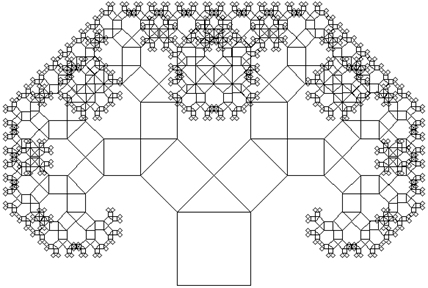
Если заменить квадраты на прямоугольники, то дерево будет больше похоже на настоящее.

Кривая Коха
Еще один классический фрактал, который строится на линиях, но результат получается в виде кривой. Для этого нужно отрезок условно разделить на 4 равные части и сложить в виде ребра треугольной формы (итерация №1). Далее каждый из полученных четырех отрезков снова сложить в виде ребра (итерация №2) и т.д. Уже на третьей итерации начинается прорисовываться еще не фигура, но уже и не отрезок. Один из лучших примеров проявления кривой Коха в природе – структура береговых линий. На километровом отрезке побережье выглядит столько же изрезанным, как и на стокилометровом.

Кривую Коха можно замкнуть в форме снежинки. Для этого нужно сложить три отрезка в виде равностороннего треугольника и на каждой стороне получить кривую Коха как в предыдущем примере. При бесконечном делении снежинка (или остров) Коха будет иметь бесконечный по длине периметр, который ограничивает конечную площадь.

Кривая Гильберта
Классическая фрактальная кривая, носящая имя немецкого математика Давида Гильберта.

Условно бесконечная нить заполняет площадь квадрата, проходя через каждую точку этой площади.

А этот кубик можно просто расправить в линию и мы не пропустим ни одной точки с необходимым нам разрешением.
Кубик Гильберта

Главное свойство, благодаря которому используется кривая Гильберта, - расстояние между двумя любыми соседними точками на кривой равно единице. Это позволяет управлять цветовой палитрой на экране монитора. Конкретнее, позволяет создавать наборы цветов для графических редакторов с отсутствием пропусков оттенков, но с шагом, достаточным для различения.
Треугольник Серпинского
Это простейший фрактал канторова множества, равное трем копиям самого себя, где каждая копия делается в два раза меньше.


Классический дырявый квадрат (ковер, салфетку) Вацлава Серпинского можно получить, к примеру, делением квадрата на 9 частей и выбрасыванием центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т. д.

Обобщение ковра Серпинского в трехмерное пространство создает губку Менгера. Каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших.

Дракон Хартера
Это фрактал, для получения которого достаточно иметь листочек бумаги в клетку и карандаш. Для его построения берется отрезок. Повернув его на 90 градусов вокруг одной из вершин и добавив полученный отрезок к исходному, получим уголок из двух отрезков. Повторим описанную процедуру. Повернем уголок на 90 градусов вокруг вершины и добавим полученную ломаную к исходной и т.д.

При достаточно большом повторении получается кривая в виде дракона.

Множества Жюлиа и Мандельброта
Дракончиков можно получить иным способом.

Все выше описанные фракталы представляют множества действительных чисел. Когда на числовой оси становится «тесно», числа выходят на комплексную плоскость. В этом случае итерацию приходится проводить для уравнений в виде полиномов, например, второго порядка:

Многоликость множество Жюлиа зависит от комплексной переменной «с».

Приведенная последовательность может уходить в бесконечность либо стремиться к некоторой конечной точке комплексной плоскости, называемой аттрактором – к пределу последовательности полинома. Множество всех точек плоскости с конечными аттракторами и называется множеством Жюлиа. Так при значении «с», равному мнимой единице i, получается вот такой красочный ковер:

При некоторых значениях «с» множество Жюлиа теряет связность и рассыпается на мелкие осколки – пыль Фату. Если множество свя́зно, то оно превращается в множество Мандельброта – в один из самых известных фракталов. В центре находится кардиоида или сердце фрактала, которое облеплено почками, наростами и причудливыми усами. Эти почки и наросты в свою очередь облеплены более мелкими почками и так далее.

Показанный на полях почтового блока жук Бенуа Мандельброта самоподобен. Строго математически изображения множеств Мандельброта и Жюлиа должны быть черно-белыми – точка либо принадлежит множеству (черный цвет), либо нет. Но были предложены варианты сделать изображения цветными. Самым распространенным способом является окрашивание точек около внешней границы множества в зависимости от количества итераций. Но Бенуа интересовала именно черная зона! Не окрестность с красивыми цветными протуберанцами, а именно скучная черная часть.
Существует такой простой шуточный тест. Глядя на эту визитку мира фракталов, нужно ответить на простой вопрос: «Что здесь самое важное – черное или цветное?».

Если ответ будет «цветное», то вы, скорее всего, в душе дизайнер. А если «черное», то вы самый настоящий и занудный математик.
Материал подготовлен по серии почтовых марок Макао 2005 года, приуроченной к Году науки и технологий.
Александр Платонов
Другие статьи автора:
С радиацией по жизни
Коллекция без претензий
Что в имени моем тебе…
Из историии мореплавания
Все гениальное просто. Или нет?
Едут-едут по Пекину наши казаки
Созвездие кактусов
Исаак Ньютон и его яблоко
Певец русской природы
А рельсы-то, как водится, у горизонта сходятся
Мятежный «Баунти». По следам золотоносного «Оскара»
Красота и привлекательность Фибоначчи
Из истории изобретения автомобиля
Отсюдова и дотудова. Почему мы так измеряем
Первая энциклопедия математических знаний России
Вильгельм Рентген и его всепроникающие Х-лучи
Самое непростое простое солнечное вещество
От Ламарка до… Ламарка
Электричество, которое сначала открыли, а затем изобрели
Гении великого вращения